什么是反函数,揭示函数与反函数的生成与性质

你有没有想过，数学世界里竟然也有一种神奇的“镜子”，它能将一个函数的输入输出颠倒过来，这就是我们要聊一聊的反函数啦！想象你把一个苹果切成两半，每一半都能反映出另一半的样子，就像镜子一样。在数学的世界里，反函数就像是这样一个神奇的“镜子”，它能让函数的图像颠倒过来，真是神奇极了！

什么是反函数？

首先，得先弄清楚什么是函数。简单来说，函数就是将一个数（我们叫它输入）映射到另一个数（我们叫它输出）的一种规则。比如，如果你有一个函数f(x)，那么f(2)可能等于4，f(3)可能等于9，这就是函数的基本样子。

而反函数，就是将这个映射颠倒过来的规则。如果有一个函数f(x)，它的反函数记作f^(-1)(x)，那么f^(-1)(4)可能等于2，f^(-1)(9)可能等于3。也就是说，反函数能够将函数的输出映射回输入。

反函数的寻找

想要找到一个函数的反函数，可不是那么容易的事情。首先，这个函数必须是一对一的，也就是说，每个输入只能对应一个输出。如果你有一个函数，比如f(x) = x^2，那么f(2)和f(-2)都等于4，这就不是一对一的，所以它没有反函数。

其次，这个函数还得是单射的，也就是说，每个输出只能对应一个输入。如果你有一个函数，比如f(x) = x^2，那么f(2)和f(-2)都等于4，这就不是单射的，所以它也没有反函数。

只有当函数既是单射又是满射的时候，它才有反函数。满射的意思是，函数的输出覆盖了所有可能的值。比如，函数f(x) = x^2在x为正数时是满射的，因为它可以覆盖所有正数。

反函数的性质

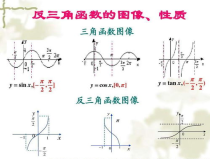
反函数有几个有趣的性质。首先，反函数的图像是原函数图像关于直线y=x对称的。想象你把一张纸对折，直线y=x就是折痕，那么反函数的图像就在折痕的另一边。

其次，反函数的图形和原函数的图形在坐标系中是互换位置的。也就是说，如果你把一个函数的图像沿着y=x这条线翻转，就能得到它的反函数图像。

反函数的名称也很有趣。如果你有一个函数f(x)，它的反函数记作f^(-1)(x)，那么f^(-1)(f(x)) = x，f(f^(-1)(x)) = x。这就是说，反函数和原函数互为对方的反函数，它们相互映射，就像一对双胞胎。

反函数的应用

反函数在数学和实际生活中都有很多应用。在数学上，反函数可以帮助我们解决一些复杂的问题，比如解方程。在现实生活中，反函数可以用来设计各种设备，比如密码锁、安全系统等。

举个例子，如果你有一个密码锁，它的密码是一个数字，那么这个数字就是一个输入，而锁的开启就是一个输出。如果你想要找到这个密码，你就可以使用反函数来解这个密码锁。

反函数就像是数学世界中的一面神奇的“镜子”，它能够将函数的输入输出颠倒过来。虽然寻找反函数需要满足一定的条件，但一旦找到了，它就能给我们带来很多便利。所以，下次当你看到数学问题中涉及到函数和反函数时，不妨停下来，想象一下这面神奇的“镜子”，也许你会对数学有更深的理解呢！